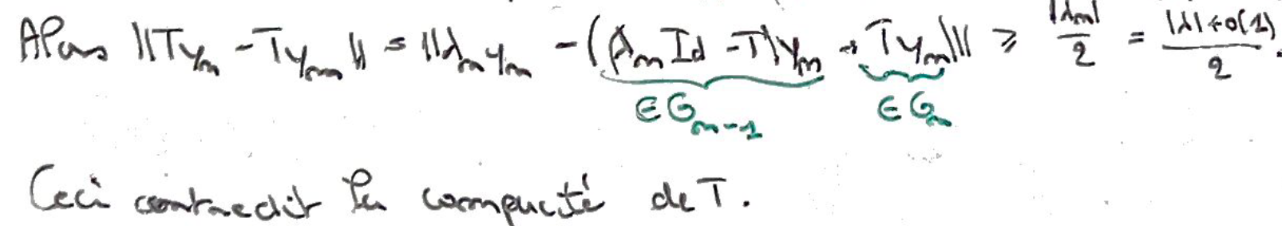Alternative de Fredholm

Alternative de Fredholm :

$E$ est un Espace de Banach
$T\in L_C(E,F)$ est un Opérateur linéaire compact
$\ker(\lambda\operatorname{Id}-T)=\{0\}$

$$\Huge\iff$$

$\operatorname{Im}(\lambda\operatorname{Id}-T)=E$
$\lambda\operatorname{Id}-T$ a un inverse continu

Valeur spectrale

Versions précisées

Alternative de Freholm précisée 1 :

$E$ est un Espace de Banach
$T\in L_C(E,F)$ est un Opérateur linéaire compact
$\operatorname{dim}(E)=+\infty$

$$\Huge\iff$$

$0\in\sigma(T)$

Alternative de Freholm précisée 2 :

$E$ est un Espace de Banach
$T\in L_C(E,F)$ est un Opérateur linéaire compact
$\lambda\in\sigma(T)\setminus\{0\}$

$$\Huge\iff$$

$\lambda$ est valeur propre : $$\exists x\in E\setminus\{0\},\quad Tx=\lambda x$$

Alternative de Freholm précisée 3 :

$E$ est un Espace de Banach
$T\in L_C(E,F)$ est un Opérateur linéaire compact
$\lambda\in\sigma(T)$

$$\Huge\iff$$

$$\exists m(\lambda)\in{\Bbb N},\quad\ker((\lambda\operatorname{Id}-T)^{m(\lambda)})=\ker((\lambda\operatorname{Id}-T)^{m(\lambda)+1})$$
$\operatorname{dim}(\ker((\lambda-\operatorname{Id})^{m(\lambda)}))\lt +\infty$

Alternative de Freholm précisée 4 :

$E$ est un Espace de Banach
$T\in L_C(E,F)$ est un Opérateur linéaire compact

$$\Huge\iff$$

$\sigma(T)$ est dénombrable
$\sigma(T)\subset B^\prime(0,\lVert T\rVert)$
$0$ est le seul Point d'accumulation possible

Démonstration de l'alternative de Fredholm précisée (3) :

On note $F_m$ le noyau à la puissance $m$ $\to$ on a immédiatement la croissance.

Supposons par l'absurde que ces inclusions sont strictes $\forall m$.

Par le Lemme de Riesz (ok car les inclusions sont strictes), $\forall m$, il existe un élément de $F_m$ assez loin de $F_{m-1}$.

La suite des images successives n'est donc pas de Cauchy, et n'admet aucune sous-suite convergente, ce qui contredit la compacité de $T$ $\to$ c'est absurde, donc le noyau est bien stationnaire.

Pour $x\in F_m$, on a une égalité semblable à celle d'un vecteur propre, mais avec un polynôme.

Une boule centrée en $0$ intersectée avec $F_m$ est donc incluse dans un compact, donc compacte.

Le Théorème de Riesz nous permet alors de conclure sur la dimension de $F_m$.

Démonstration de l'alternative de Fredholm précisée (4) :

Pour $\lvert\lambda\rvert\gt \lVert T\rVert$, on a un développement en série entière de $(\lambda\operatorname{Id}-T)^{-1}$.

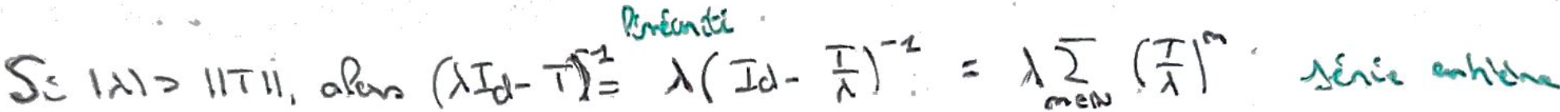
C'est un inverse continu, ce qui fait que $\lambda$ n'est pas une Valeur spectrale.

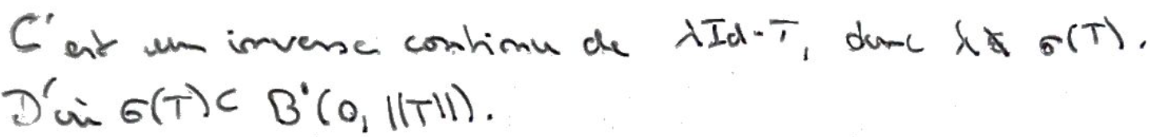
Par l'absurde, considérons une suite injective de $\sigma(T)$ tendant vers un point non nul (caractérisation d'un Point d'accumulation).

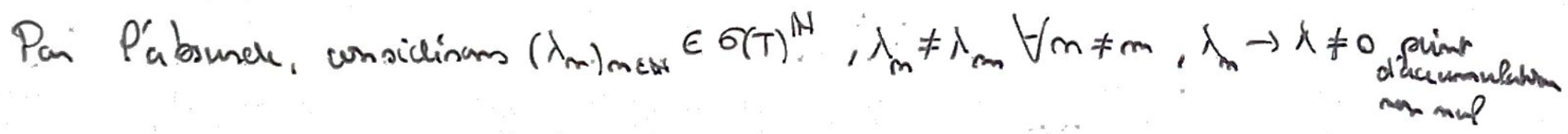
Pour tout rang $n$, on considère le "vecteur propre" unitaire associé à $\lambda_n$.

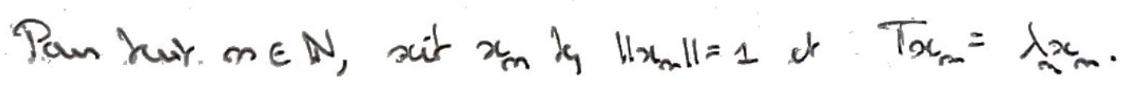
On pose $(G_N)_N$ la suite des espaces vectoriels engendrés par $x_1,\dots,x_N$.

Cette suite est croissante, et les inclusions sont strictes puisque les vecteurs propres sont associés à des valeurs propres distinctes.

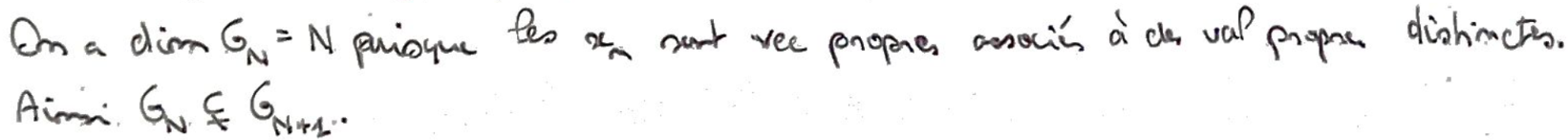
On peut donc utiliser le Lemme de Riesz entre $G_n$ et $G_{n+1}$, avec un vecteur unitaire.

On a alors une suite qui n'a pas de sous-suite convergente, ce qui contredit la compacité de $T$ $\to$ pas de point d'accumulation non nul.

Math'φsics

Formulaire de report

Versions précisées